Index

(1) \(U,\;W\)是数域\(F\)上的向量空间。试证：集合\(U{\times}W\)是向量空间，其元素满足等式\((u,w)+(u',w')=(u+u',w+w')\)和\(c(u,w)=(cu,cw)\)其中\(u{\in}U,\;w{\in}W\)

(2) 设\(U,W\)均为向量空间\(V\)的子空间，试证：由\(T(u,w)=u+w\)定义的映射\(T:U{\times}W{\rightarrow}V\)是线性变换。

(3) 用\(V\)的子空间的维数表示\(T\)的维数方程。

(1) 对集合\(U{\times}W\)中的任意两个元素\((u,w),\;(u',w')\)，数域\(F\)上的任意数\(c\)，验证向量空间的条件：
因为\(U,\;W\)是向量空间，故\((u+u'){\in}U,\;cu{\in}U\)，\((w+w'){\in}W,\;cw{\in}W\)，则\((u+u',w+w'),\;(cu,cw){\in}U{\times}W\)，于是题设中两个等式即加法和数乘运算。
交换律 \((u,w)+(u',w')=(u+u',w+w')=(u'+u,w'+w)=(u',w')+(u,w)\)成立，单位向量为\((0,0)\)
单位运算： \(1(u,w)=(1u,1w)=(u,w)\)
结合律： \((ab)(u,w)=((ab)u,(ab)w)=(a(bu),a(bw))
=a(b(u,w)),\;a,b{\in}F,\;(u,w){\in}\
U{\times}W\)
分配律： \begin{align*}(a+b)(u,w)&=((a+b)u,(a+b)w)=(au+bu,aw+bw)\\&=(au\
,aw)+(bu,bw)=a(u,w)+b(u,w)\\a((u,w)+(u',w'))&=a(u+u',w+w')=(a(u+u'),a(w+w'))\\&\
=(au+au',aw+aw')=(au,aw)+(au',aw')\\&=a(u,w)+a(u',w'),\;a{\in}F,\;(u,w),(u',w')\
{\in}U{\times}W\end{align*}

(2) 证明：\(T((u,w)+(u',w'))=T(u+u',w+w')=(u+w)+(u'+w')=T(u,w)+T(u',w'),\;T(c(u,w))=T(cu,cw)=cu+cw=c(u+w)=cT(u,w),\;c{\in}F\)得证。

(3)（对不对呢？） \begin{align*}
\text{dim}(\text{ker}\;T)&=\text{dim}(U\cap W)\\
\text{dim}(\text{im}\;T)\;&=\text{dim}(U)\text{dim}(W)-\text{dim}(U)\text{dim}(U\cap W)-\text{dim}(W)\text{dim}(U\cap W)+\text{dim}^2(U\cap W)\\&+\text{dim}(U)\text{dim}(U\cap W)-\text{dim}^2(U\cap W)+\text{dim}(W)\text{dim}(U\cap W)-\text{dim}^2(U\cap W)\\&+{\large C}_{\text{dim}(U\cap W)}^2\\&=\text{dim}(U)\text{dim}(W)-\text{dim}^2(U\cap W)+\frac{1}{2}(\text{dim}^2(U\cap W)-\text{dim}(U\cap W))\\&=\text{dim}(U)\text{dim}(W)-\frac{1}{2}\text{dim}^2(U\cap W)-\frac{1}{2}\text{dim}(U\cap W)\\
\text{所以，所求}&\text{维数方程是：}\\
\text{dim}(U)&\text{dim}(W)-\frac{1}{2}\text{dim}^2(U\cap W)+\frac{1}{2}\text{dim}(U\cap W)=\text{dim}(U\times W)
\end{align*}

试证：所有的秩为1的\(m{\times}n\)阶矩阵\(A\)都能表示成\(A = XY^t\)的形式，其中\(X,Y\)分别是\(m\)阶，\(n\)阶列向量。试说明这种表示形式是否唯一。

证明：首先证明\(A\)的列向量\(v_1,v_2,\cdots,v_n\)中任意两个都线性相关。因为矩阵\(A\)的秩是1,所以由\(A\)的所有列向量扩展成的线性空间的基可以是\(A\)的列向量中任意一个非零向量。因此，\(A\)的列向量都能表示成所选定的基的倍数。\(A=(A_1,A_2,\cdots,A_n)\)假设\(A_i{\ne}0\;(1{\leqslant}i{\leqslant}n)\)，可得
\begin{align*}
A&=(A_1,A_2,\cdots,A_n)\\&=(A_iy_1,A_iy_2,\cdots,A_iy_n)\\&=A_i(y_1,y_2,\cdots,y_n)
\end{align*}
题设得证。
\(X\)可以是\(A\)中任意非零列向量，表示形式不唯一。

\(A\)是\(m{\times}n\)阶矩阵（\(n>m\)），利用维数公式证明：线性方程组\(AX=0\)的解的维数至少是\(n-m\)。

证明：线性变换\(T:V{\rightsquigarrow}W\)由\(AX\;(X{\in}V)\)定义。显然，\(V\)的维数是\(n\)。\(T\)的核ker\((T)\)是线性方程组\(AX=0\)的解系的维数（根据核的定义），\(T\)的像im\((T)\)是\(A\)的列向量空间。方程组\(AX=0\)的系数矩阵\(A\)化成阶梯形后的非零行数至多是\(m\)，可知im\((T)\)\({\leqslant}m\)因此，根据维数公式dim(ker \(T\))+dim(im \(T\))=dim\((V)\)，dim(ker \(T\))=dim\((V)\)-dim(im \(T\))\({\geqslant}n-m\)。

向量空间\(V\)中的元素\(v_1,v_2,\cdots,v_n\)，证明规则\(\phi(X)=v_1x_1+\cdots+v_nx_n\)定义的映射\(\phi:F^n{\rightarrow}V\)是线性变换。(\(X=(x_1,x_2,\cdots,x_n)^t\)是数域\(F\)上的列向量）

证明：空间\(F^n\)中的任意元素\(Y=(y_1,y_2,\cdots,y_n)^t,\;Z=(z_1,z_2,\cdots,z_n)^t\)，于是
\begin{align*}
\phi(Y+Z)&=v_1(y_1+z_1)+v_2(y_2+z_2)+\cdots+v_n(y_n+z_n)\\&=(v_1y_1+v_2y_2+\cdots+v_ny_n)+(v_1z_1+v_2z_2+\cdots+v_nz_n)\\&=\phi(Y)+\phi(Z)\\
\\
\phi(cY)&=v_1cy_1+v_2cy_2+\cdots+v_ncy_n\\&=c(v_1y_1+v_2y_2+\cdots+v_ny_n)\\&=c\phi(Y)
v
\end{align*}
证毕。

\(A\)是\(l{\times}m\)矩阵，\(B\)是\(n{\times}p\)矩阵，证明规则\(M{\rightsquigarrow}AMB\)是一种线性变换——把线性空间\(F^{m{\times}n}\)中的元素\(m{\times}n\)矩阵变换到\(F^{l{\times}p}\)。

证明：设空间\(F^{m{\times}n}\)中的任意矩阵\(X_1,\;X_2\)，数域\(F\)中的任意数\(c\)。则依据题设规则和矩阵乘法和加法运算法则以及矩阵运算结合律、分配律可得\(A(X_1+X_2)B = AX_1B+AX_2B,\;A(cX_1)B=cAX_1B=c(AX_1B)\)，由
\(A,\;B,\;X_1,\;X_2\)的行数和列数可知\(AX_1B,\;AX_2B,\;c(AX_1B)\)均是线性空间\(F^{l{\times}p}\)中的元素。因此映射\(M{\rightsquigarrow}AMB\)满足线性变换的定义，题设成立。

\[
利用矩阵的分块乘法计算:
\left[
\begin{array}{cc|cc}
1&1&1&5\\0&1&0&1\\
\hline
1&0&0&1\\0&1&1&0
\end{array}
\right]
\cdot
\left[
\begin{array}{cc|cc}
1&2&1&0\\0&1&0&1\\
\hline
1&0&0&1\\0&1&1&3
\end{array}
\right]
\]

\[
\begin{multline*}
\begin{split}
解:原式&=
\left[
\begin{array}{c|c}
\begin{bmatrix}1&1\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}1&2\\0&1\end{bmatrix}
+
\begin{bmatrix}1&5\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}1&0\\0&1\end{bmatrix}\;
&\;
\begin{bmatrix}1&1\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}1&0\\0&1\end{bmatrix}
+
\begin{bmatrix}1&5\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}0&1\\1&3\end{bmatrix}\\
\hline
\begin{bmatrix}1&0\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}1&2\\0&1\end{bmatrix}
+
\begin{bmatrix}0&1\\1&0\end{bmatrix}
\cdot
\begin{bmatrix}1&0\\0&1\end{bmatrix}\;
&\;
\begin{bmatrix}1&0\\0&1\end{bmatrix}
\cdot
\begin{bmatrix}1&0\\0&1\end{bmatrix}
+
\begin{bmatrix}0&1\\1&0\end{bmatrix}
\cdot
\begin{bmatrix}0&1\\1&3\end{bmatrix}
\end{array}
\right]\\\\&=\left[
\begin{array}{c|c}
\begin{bmatrix}1&3\\0&1\end{bmatrix}
+
\begin{bmatrix}1&5\\0&1\end{bmatrix}\;\;
&
\begin{bmatrix}1&1\\0&1\end{bmatrix}
+
\begin{bmatrix}5&16\\1&3\end{bmatrix}\\
\hline
\begin{bmatrix}1&2\\0&1\end{bmatrix}
+
\begin{bmatrix}0&1\\1&0\end{bmatrix}\;\;
&
\begin{bmatrix}1&0\\0&1\end{bmatrix}
+
\begin{bmatrix}1&3\\0&1\end{bmatrix}
\end{array}
\right]=\left[
\begin{array}{c|c}
\begin{bmatrix}2&8\\0&2\end{bmatrix}\;
&\;
\begin{bmatrix}6&17\\1&4\end{bmatrix}\\
\hline
\begin{bmatrix}1&3\\1&1\end{bmatrix}\;
&\;
\begin{bmatrix}2&3\\0&2\end{bmatrix}
\end{array}
\right]=\begin{bmatrix}2&8&6&17\\0&2&1&4\\1&3&2&3\\1&1&0&2\end{bmatrix}
\end{split}
\end{multline*}

\]

求证：任意三角形的外心、重心、垂心共线，并且外心到重心的距离等于重心到垂心的距离的一半。

——Euler定理

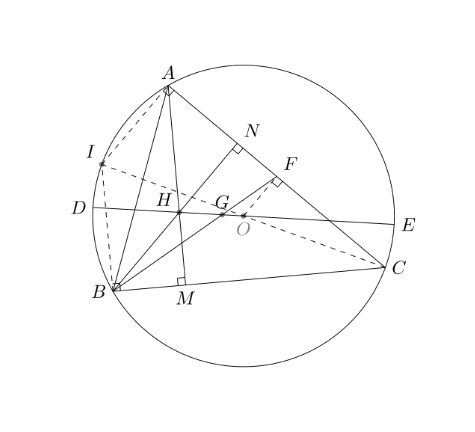
证明：

考虑锐角三角形，如图\(\triangle ABC\)的垂心\(H\)，外心是\(O\)，过\(HO\)的直线交外接圆于\(DE\)，\(F\)是\(AC\)的中点，连接\(BF\)交\(DE\)于\(G\),下面证明\(G\)是\(\triangle ABC\)的重心。

连接\(OF\)则\(\angle OFC = 90^\circ\)，连接\(CO\)其延长线交圆\(O\)于\(I\)，连接\(IA\),\(IB\)。因为\(CI\)是\(\triangle ABC\)的外接圆直径，所以\(CO=OI,\:\angle IAC=90^\circ\)，同理，\(\angle IBC=90^\circ\)。因为\(OF\perp AC,:IA\perp AC\)，所以\(OF\parallel IA\)，因此\(OF=\frac{1}{2} IA\)。